刚体转动实验
主讲教师:于文惠
课时:3学时
教材:《大学物理实验(第二版)》
简介:刚体转动的一个重要物理量是转动惯量,它是表征转动物体惯性大小的物理量。在许多研究领域和工业设计中都要考虑物体转动惯量的大小。因此,测定物体的转动惯量具有重要的实际意义。
对于形状比较规则的物体,可用数学方法计算出它的转动惯量。但对于形状比较复杂的物体,一般需用实验方法进行测定。测定转动惯量的方法很多,本实验利用刚体转动实验仪测量给定物体的转动惯量,并由此验证转动定律及平行轴定理。
实验重点:测量实验中给定系统的转动惯量。
难点:刚体绕定轴转动时转动惯量随质量及质量分布而改变的规律。
教学目的:1. 测量给定系统的转动惯量。
2.研究刚体绕定轴转动时转动惯量随质量及其分布而改变的规律。
教学方法:课堂演示
实验要求:精确测定给定系统的转动惯量。
实验仪器:刚体转动实验仪、砝码、米尺、秒表等。
本实验中所用的刚体转动实验仪,如图2-8-1所示。塔轮由不同半径圆盘组合而成的,塔轮半径共分为五个尺寸分别为,1.00cm,1.50cm,2.00cm,2.50cm和3.00cm。塔轮两边对称伸出两根有等分刻度的均匀细圆柱型连杆B。连杆两端各有一个可移动的圆柱形重锤。它们一起组成一个可绕轴00’转动的刚体系。塔轮上绕一细线,跨过滑轮3,线的另一端挂有砝码5。当砝码下落时通过细线对系统施以力矩。滑轮3的高低可由固定螺丝4调整,以使细线与转动轴保持垂直。滑轮架7上的标记F是用来判断砝码起始位置的。6是固定滑轮架的螺旋板手。轴 00’的铅直可通过三个底脚螺丝S1、S2、和S3来调节。轴的松紧程度可通过螺丝8进行调节。

图2- 8-1刚体转动实验仪
实验原理:
根据转动定律,当刚体绕固定轴转动时,有
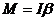 (2-8-1)
(2-8-1)
所以,如果能测出系统的合外力矩M和转动时的角加速度b,则转动惯量可由上式求出。系统的合外力矩由绳子施于塔轮上的力矩 (r 为塔轮半径,T为绳子的张力)和轴处的摩擦力矩Mu组成,如果选前者的方向为正,则M的大小为:
(r 为塔轮半径,T为绳子的张力)和轴处的摩擦力矩Mu组成,如果选前者的方向为正,则M的大小为:
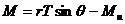 (2-8-2)
(2-8-2)
当调节绳子的方向,使它与塔轮的半径相垂直,则有sinq=1,因此有
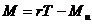 (2-8-3)
(2-8-3)
绳子的张力可用下述方法求得:若略去滑轮及绳子的质量,并认为绳子是不可伸长的,砝码m将以匀加速度a下落。根据牛顿第二定律可得到
 (2-8-4)
(2-8-4)
式中,g为重力加速度,m为砝码的质量。若砝码m在高度h的地方从静止开始下落,到达地面所用的时间为t,则有
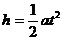 (2-8-5)
(2-8-5)
由于塔轮转动时边缘的切向加速度和砝码m下落时的加速度a相等,即
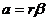 (2-8-6)
(2-8-6)
由以上关系式,可得刚体合外力矩为
 (2-8-7)
(2-8-7)
实验中,若保持 a <<g ,则上式可简化为
 (2-8-8)
(2-8-8)
如果轴的松紧度调整合适,可认为 Mu <<mgr ,而将Mu略去,则有
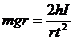 (2-8-9)
(2-8-9)
利用(2-8-8)或(2-8-9)式,就可以求得系统的转动惯量I并能验证转动定律及平行轴定理。
下面分别讨论几种情况:
①将(2-8-8)式改写成如下形式
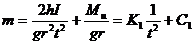 (2-8-10)
(2-8-10)
式中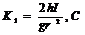 1=
1=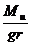 。由(2-8-10)式知,m与t2成反比。实验中若保持 r、h及 I 不变,并设Mu亦不变。改变m测出相应的下落时间 t,在坐标纸上作 m---t-2图,如得到一直线,则由实验结果证明转动定律成立。由斜率K1可求得I ,由截距C1可求得Mu。
。由(2-8-10)式知,m与t2成反比。实验中若保持 r、h及 I 不变,并设Mu亦不变。改变m测出相应的下落时间 t,在坐标纸上作 m---t-2图,如得到一直线,则由实验结果证明转动定律成立。由斜率K1可求得I ,由截距C1可求得Mu。
②实验中,若保持 r、h 及 m不变,对称地改变m0的质心距轴 00’的距离x,由刚体转动惯量的平行轴定理可知,整个转动系统对00’轴的转动惯量为
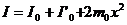 (2-8-11)
(2-8-11)
式中,I。为连杆2和塔轮1绕 00’轴的转动惯量,I。’为两个圆柱体绕过其质心且平行于 00’轴的转动惯量。将上式代入(2-8-9)中得到
 (2-8-12)
(2-8-12)
式中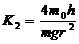 ,
,
若考虑Mu并设其不变,可将式(2-8-11)代入式(2-8-8)则有
 (2-8-13)
(2-8-13)
式中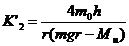 ,
,
在坐标纸上作 t2----x2 图可证明平行轴定理。
实验步骤:
1.安装和调节实验装置,调整座架呈水平,适当调节螺丝,以使转动系统灵活,固定好m。,调节滑轮的高度等。
2.选取塔轮半径r =2.50cm,m。置于(5,5')位置,依次取砝码的质量为10克、20克、30克、40克、50克(砝码托质量5.00克,每个砝码质量5.00克),用停表测从F处开始下落到地面所需时间t,对每个m测量三次求平均值。将数据填入表2-8-1中。注意,当m较小时,由于摩擦力矩的影响较大,测出的t的重复性较差。随着m等量增加,t 是逐渐减小的,而减小的量越来越小。由实验结果作出m--1/t2图,求出转动惯量 I 及摩擦力矩Mu,验证转动定律。
3.选取塔轮半径r 为2.50 cm,砝码质量m为20克,对称地改变m0的位置,使其分别位于(1,1’)、(2,2’)、(3,3’)、(4,4’)、(5,5’)处,测出相应的时间t。将数据填入表2-8-2。观察转动惯量与质量分布的关系。作出t2—x2图。验证平行轴定理。
实验数据:
表2-8-1验证转动定律数据表
r= cm; m。位于5,5’位置; h= cm
t(s)m(g) |
10.00 |
20.00 |
30.00 |
40.00 |
50.00 |
t1 |
|
|
|
|
|
t2 |
|
|
|
|
|
t3 |
|
|
|
|
|

|
|
|
|
|
|

|
|
|
|
|
|
作m---1/t2图。
实验结果:斜率 K = 转动惯量I=
表 2-8-2 验证平行轴定理数据表
m= g; h = cm
m0位置 |
1,1’ |
2,2’ |
3,3’ |
4,4’ |
5,5’ |
x |
|
|
|
|
|
t |
|
|
|
|
|
x2 |
|
|
|
|
|
t2 |
|
|
|
|
|
作出 t2-----x2图。
注意事项:
1.了解秒表的使用程序是一走、二停、三回零。正确地使用秒表计时(机械表使用前上满弦,用后放弦)。
2.实验前应先检查00’轴线是否保持垂直。方法是取下待测刚体部分,换上校准重锤,旋转底脚螺丝S1,使锤尖对准轴碗心即可。
3.作图时应注意按测量数据选择合适的坐标纸,数据的最末一位准确数字应与图上的最小刻度线相对应。以自变量、因变量画出横、纵坐标轴,并标明方向及所代表的物理量。