拉伸法测金属丝的杨氏模量
课时:3学时
教材:《大学物理实验》钟鼎主编
简介:
材料在“弹性限度内”,金属丝单位截面积上的作用力F/S与它的相对形变量ΔL/L的比值称为杨氏模量(Young‘s Modulus)。它是描述金属材料抵抗形变能力的物理量,在工程上作为选择材料的依据之一。
由于这个形变量一般很小,用通常的测长仪器难以测准,故本实验采用光杠杆法。光杠杆原理已经被广泛地应用于灵敏度高的仪器上(如冲击电流计、光点式检流计等)作为测量角度微小的改变量。
在数据处理上,本实验采用逐差法,它是处理某些形变量的多次测量的有效方法。
实验重点:掌握用光杠杆法测量微小变化量的方法。
难点:微小测量量的装置调整。
教学目的:1. 测定金属丝的杨氏模量。
2.学会用光杠杆测量微小的长度变化。
3.熟悉用逐差法处理数据。
教学方法:以学生实验操作为主,集中讲解、演示,巡回指导。
实验要求:1.课前预习,完成预习报告;能够回答实验相关问题。
2.课堂上独立操作完成实验,解决实验中遇到的问题,完成思考题。
3.课后完成实验报告,做出实验总结。
实验仪器:杨氏模量测定仪及砝码、螺旋测微计、游标卡尺、卷尺
实验原理:
如果在外力F作用下,原长L、截面积S的金属丝在弹性限度内产生形变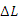 ,则杨氏模量
,则杨氏模量
 (1)
(1)
 可见测量的关键是
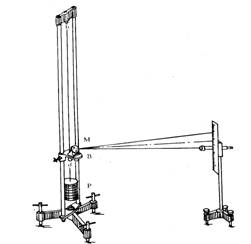
可见测量的关键是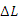 。图l是杨氏模量测定仪。图中左边称为伸长仪,右边称为镜尺组。被测金属丝夹持在b、d之间。d是一个可在平台B的中心圆孔内上下移动的圆柱形的夹持件,其下端是施加外力的法码P。在平台上放置一个有三足尖的反射镜M(光杠杆),它的后足尖位于夹持件d上,而前两足尖置于平台的沟槽内。当勾码上加减砝码时,就可改变反射镜的倾角。
。图l是杨氏模量测定仪。图中左边称为伸长仪,右边称为镜尺组。被测金属丝夹持在b、d之间。d是一个可在平台B的中心圆孔内上下移动的圆柱形的夹持件,其下端是施加外力的法码P。在平台上放置一个有三足尖的反射镜M(光杠杆),它的后足尖位于夹持件d上,而前两足尖置于平台的沟槽内。当勾码上加减砝码时,就可改变反射镜的倾角。

 如图2所示,如果在测量前将反射镜M的镜面调成与望远镜垂直,即望远镜中能看到直尺
如图2所示,如果在测量前将反射镜M的镜面调成与望远镜垂直,即望远镜中能看到直尺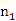 处的反射像;当加砝码时,由于金属丝被拉长,夹持件d下降,而导致光杠杆的后足尖下降一段距离
处的反射像;当加砝码时,由于金属丝被拉长,夹持件d下降,而导致光杠杆的后足尖下降一段距离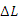 (即金属丝的伸长量),同时镜面转过微小角度
(即金属丝的伸长量),同时镜面转过微小角度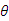 ,则此时从望远镜中能看到直尺
,则此时从望远镜中能看到直尺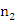 处的反射像。由几何可得
处的反射像。由几何可得
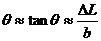
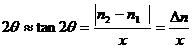
即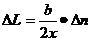
其中 为镜尺距离,b为光杠杆的杆长,将其代入式(1),并考虑到对金属丝
为镜尺距离,b为光杠杆的杆长,将其代入式(1),并考虑到对金属丝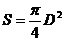 (D为直径)得出
(D为直径)得出
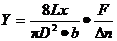 (2)
(2)
如果长度单位采用m,力的单位采用N,则Y的单位为Pa。
实验步骤:
1.用水平仪把杨氏模量测定仪调成铅直。
2.在试件下部挂上砝码托,以便拉直试件。
3.将光杠杆放在小平台上(前足尖置于沟槽内,后足尖放在小圆柱体上,但不能触碰试件),将望远镜调成大致与反射镜面中心等高。
4.调整望远镜的目镜,使能看清楚十字叉丝,转动镜筒使叉丝横平竖直。
5.旋转望远镜物镜直至从望远镜中看清楚标尺刻度为止。为了调节方便,可将眼睛位于望远镜的上方,顺着镜筒的方向观察,看反射镜内有无标尺的像。如没有,可左右移动标尺组支架,直到出现标尺像。
6.调整反射镜面的仰角,使其尽量铅直并记下此时标尺的读数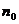 。
。
7.每一次加一个砝码(2kg),按表1记下相应的标尺读数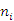 。再依次减一个砝码并记下标尺读数。
。再依次减一个砝码并记下标尺读数。
8.在金属丝的不同位置测量直径六次。
9.测金属丝长度L、平面反射镜前足尖与直尺间距离 及光杠杆杆长b各一次。其中b的测量可以这样来做,在纸上压出三足尖的位置,用作垂线的方法量出长度。
及光杠杆杆长b各一次。其中b的测量可以这样来做,在纸上压出三足尖的位置,用作垂线的方法量出长度。
天津地区重力加速度的标准值g = 9.80101 m/s2
实验数据:
表1 杨氏模量测量数据表(一)
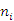 (×10-3mm) (×10-3mm)
|
F(N) |
0 |
2kg |
4kg |
6kg |
8kg |
10kg |
增加 |
|
|
|
|
|
|
减少 |
|
|
|
|
|
|
平均值 |
|
|
|
|
|
|
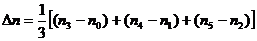
表2 杨氏模量测量数据表(二)
千分尺零点读数:(×10-3m)
测量次数 |
1 |
2 |
3 |
4 |
5 |
6 |
直径测量值 |
|
|
|
|
|
|
修正值 |
|
|
|
|
|
|
平均值 |
|
|
|
|
|
|
L= (m); = (m);b= (m)
= (m);b= (m)
将各数据代入式(2),求出Y的大小(暂不定位数)。
用估计法确定误差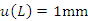 ,
, 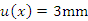 ,
,  ,然后利用误差传递公式求出:
,然后利用误差传递公式求出: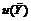
测量结果用  表示。
表示。
金属丝的杨氏模量参考值为: 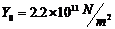 ,把实验值与
,把实验值与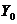 作一比较。
作一比较。
注意事项:
1. 调整反射镜面的倾度应合适(以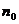 不超过刻度10为限),否则会使读数值超出标尺的上限(25mm)。
不超过刻度10为限),否则会使读数值超出标尺的上限(25mm)。
2. 在同一砝码的增、减两种情况下,标尺读数可能不一样,这是正常的,这是由于试样形变量需一段恢复时间的缘故。
3. 实验时,砝码的取放要轻,以减少试件的振动,便于读数。